What's behind the couch?
Directed Ray Distance Functions for 3D Scene Reconstruction


Nilesh Kulkarni
Justin Johnson
David F. Fouhey

University of Michigan, Ann Arbor

ECCV 2022

[pdf]
[code]
[video]

Our approach generates 3D from a single unseen input image (left) while training on real 3D scans. We show the two rendered novel views of our output (middle, right). Visible surfaces are colored by the image and occluded ones are colored with surface normals: pink is upwards and lavender faces the camera. We can observe the occluded cabinet and floors behind the couch predicted my our approach visible in novel views.


Sample results generated by our model on unseen images from Matterport3D dataset. DRDF is able to recover occluded parts of the floor by the kitchen top, couch, bed. It can recover complete empty rooms behind walls. It also recovers parts of the scene where GT has holes (behind the couch )

Overview
We present an approach for scene-level 3D reconstruction, including occluded regions, from an unseen RGB image. Our approach is trained on real 3D scans and images. This problem has proved difficult for multiple reasons:
  • Real scans are not watertight, precluding many methods
  • Distances in scenes require reasoning across objects (making it even harder)
  • Uncertainty about surface locations motivates networks to produce outputs that lack basic distance function properties
We propose a new distance-like function that can be computed on unstructured scans and has good behavior under uncertainty about surface location. Computing this function over rays reduces the complexity further. We train a deep network to predict this function and show it outperforms other methods on Matterport3D, 3D Front, and ScanNet


Interactive Demo - 3D Models
We present predicted 3D model from our approach using an interactive visualizer. Our model takes input the image and generates the output under DRDF.

Demo Instructions
  • To disable the model uncheck the "Enable interactions" box.
  • To interact with the ground-truth and DRDF outputs independently uncheck "Tie Controls" box.
  • Click on the models to view them from different angles.

Choose a demo and click on the models to interact!

Tie Controls


Additional interactive results on examples from Matterport3D and 3DFront

Interactive Demo - Distance Functions
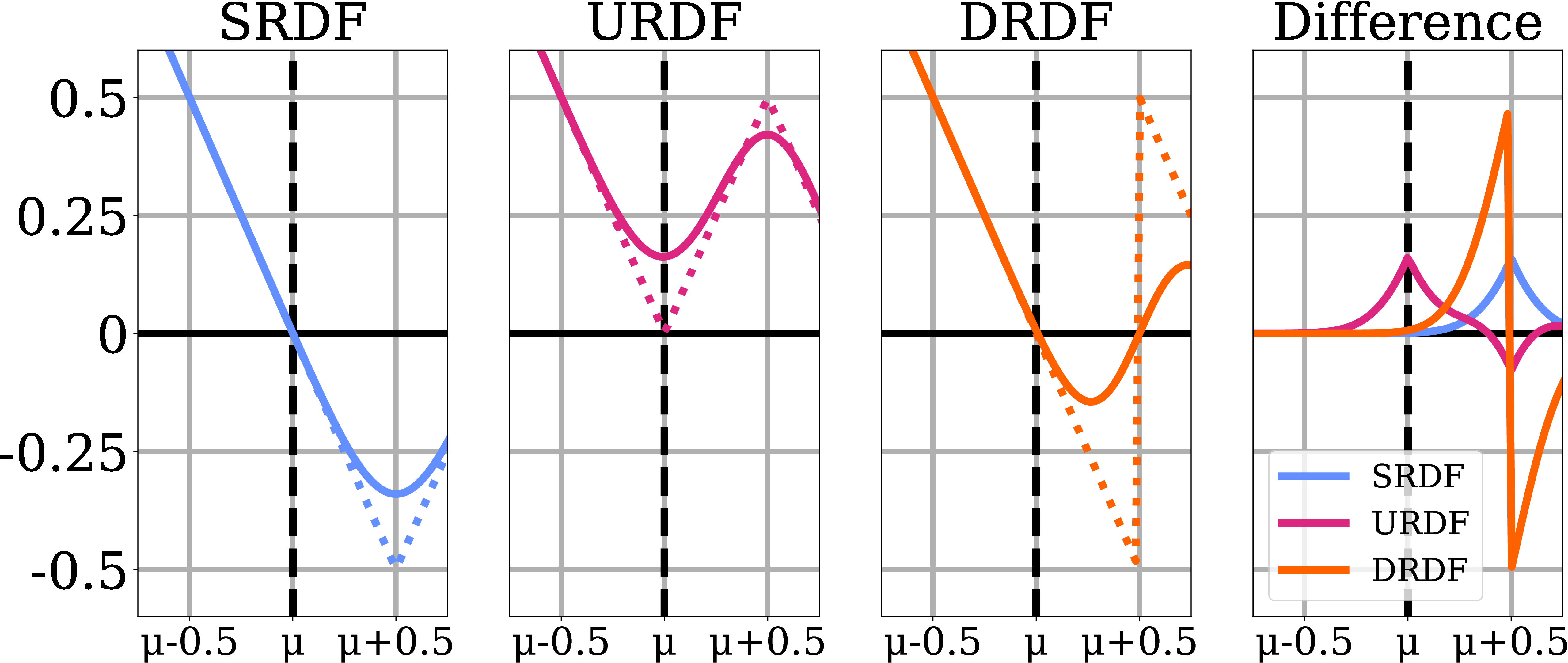
We analyse the behavior of distance functions in 1D case for ray going from -∞ to ∞. This ray intersects at two locations μ and μ+1 along the x-axis. We plot the Signed Ray Distance Function (SRDF), Unsigned Ray Distance Function (URDF), Directed Ray Distance Function (DRDF) using a dashed line (— — —). We add noise to the intersection location (μ) using the Gaussian distribution and compute the expectation of these distance functions under this distribution (shown with a ——— line).

Neural networks trained to mimic these distance functions with MSE minimizer are optimal when they produce the expected distance function. Expected distance functions lack the crucial properties of distance functions (like norm of gradients is 1). This disparity increases with more uncertainty. Hence, outputs of neural networks do not behave like actual distance functions. For instance, in case of URDF the expected distance function has the highest error at the location of the intersection μ. While the expected DRDF and SRDF also do not mimic the actual distance function their errors tend to occur away from the intersection in case of uncertainty.

Using SRDF is not possible for real data as it is not watertight. Our proposed DRDF has low error at the location of the intersection and most of the error is pushed towards the mid way between the intersections. This property of DRDF allows us to recover intersections with a simple inference strategy of detecting +ve to -ve zero crossings along the ray.


Below we show an interactive demo of all the distance functions and how they are affected by noise. Move the slider with noise around to see the behavior of expected distance functions with respect to noise

Noise Standard Deviation 00.3
Uncertainty About Intersection SRDF (Impossible) URDF DRDF (Proposed)

Approach
We present an approach to train a model to predict 3D from single images using real 3D scans data and corresponding images. Below we present our core ideas.
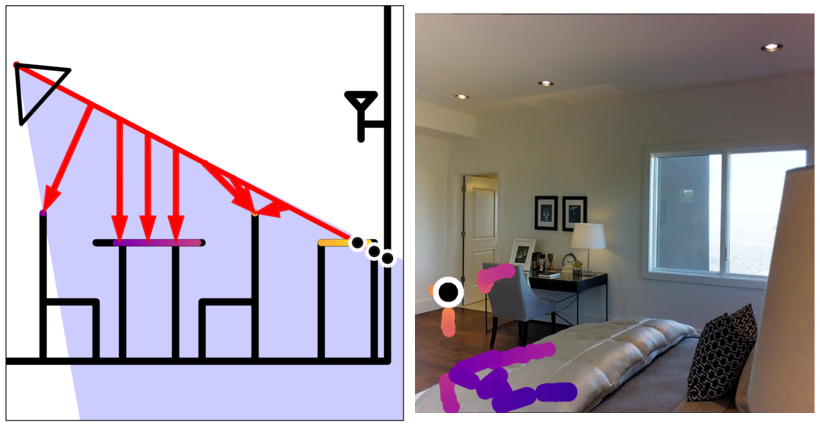
Scene vs Ray distances. We predict distances along the ray instead of distances to the scene. Predicting distances to scenes requires inference beyond pixels that are along the ray. For instance, in the 2D example, on the left, we show how the nearest points to the red ray change as we travel along the ray. We color the nearest points with the points the on the red ray they correspond. Similarly of the example image of a 3D scene we project points nearest to the ray onto the image and color them with the depth of the point on the ray.
Choice of Distance Function. We design the directed ray distance function (DRDF) and compare it in a simple scenario. Suppose the surface's location is normally distributed with mean μ at its true location and σ=0.2, and the next surface 1 is unit away. We plot the expected (solid) and true (dashed) distance functions for the SRDF, URDF, and DRDF and their difference (expected - true). The SRDF and DRDF closely match the true distance near the surface; the URDF does not. Interactive demo for this idea is above.
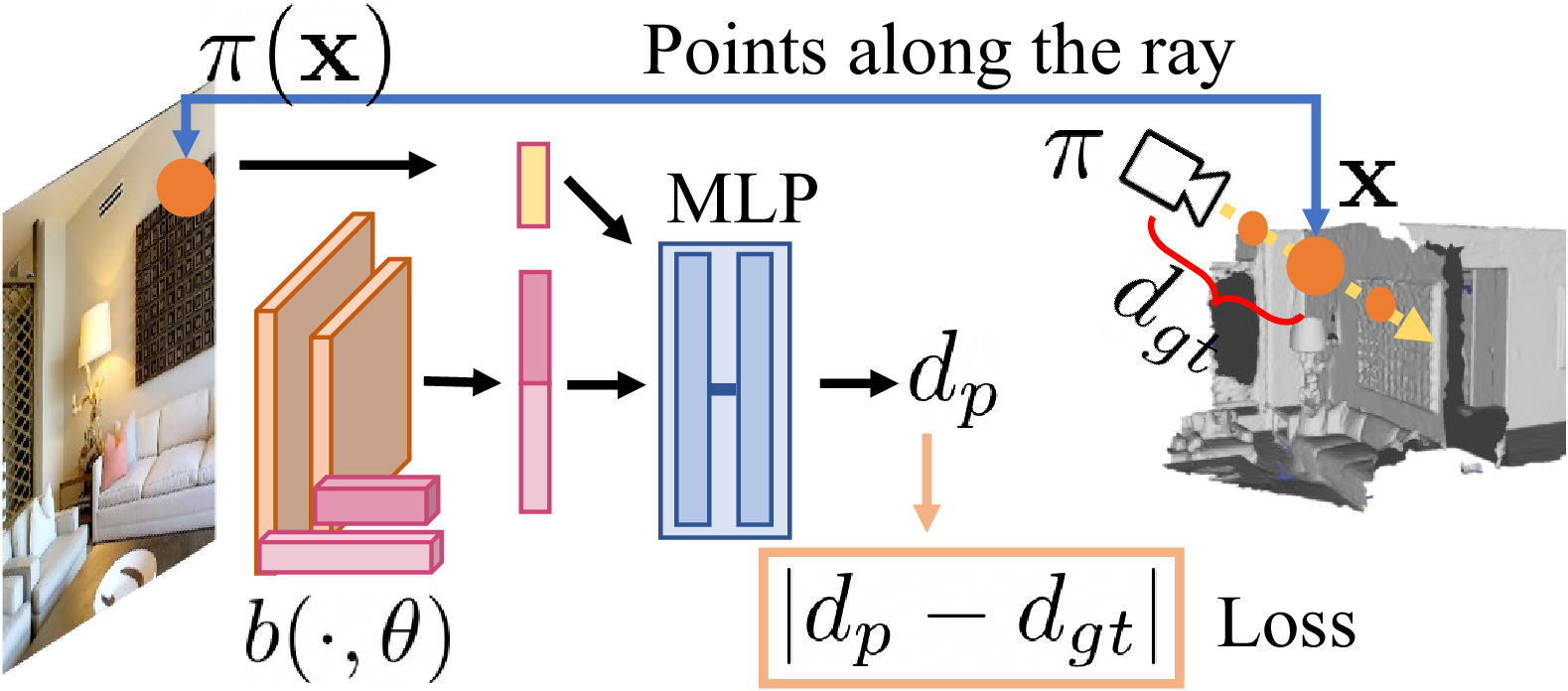
Method overview. At training time, our model takes an image and set of 3D points along rays and is supervised on the distance to the nearest intersection via the real 3D geometry. For inference, our model predicts the distance for each point in a 3D grid, which is then decoded to intersections.

Video Results
Main Paper Results Additional Results
Supplemental Results

Paper
Kulkarni, Johnson, Fouhey

What's behind the couch? Directed Ray Distance Functions for 3D Scene Reconstruction.

Arxiv, 2021

[pdf]
[bibtex]

Code

 [GitHub]

Acknowledgements

We would like the thank Alexandar Raistrick and Chris Rockwell for their help with the 3DFront dataset. We like to thank Shubham Tulsiani, Richard Higgins, Sarah Jabour, Shengyi Qian, Linyi Jin, Karan Desai, Mohammed El Banani, Chris Rockwell, Alexandar Raistrick, Dandan Shan, Andrew Owens for comments on the draft versions of this paper. NK was supported by TRI. Toyota Research Institute (''TRI'') provided funds to assist the authors with their research but this article solely reflects the opinions and conclusions of its authors and not TRI or any other Toyota entity. This base version of the template is borrowed from colorful folks.